Static vs. Distribution-Free: Chebyshev and the Empirical Rule
- May 25, 2025
- Posted by: Drglenbrown1
- Category: Trading Methodology
When designing stop-loss buffers, it’s crucial to understand both the Empirical Rule (for near-normal regimes) and Chebyshev’s Inequality (distribution-free). This article shows when you can lean on normality, why Chebyshev offers a worst-case safety net, and how our √P exposures (k≈15) map to concrete coverage guarantees.
Summary
- When the Empirical Rule (68-95-99.7) applies—and when it doesn’t
- Chebyshev’s bound:
1 − 1/k²for any distribution - Mapping k=√P exposures to guaranteed volatility coverage
Key Sections
- Side-by-Side Coverage Table
- Practical Takeaways for Stop-Loss Design
- Fitting into the Seven-Law Playbook
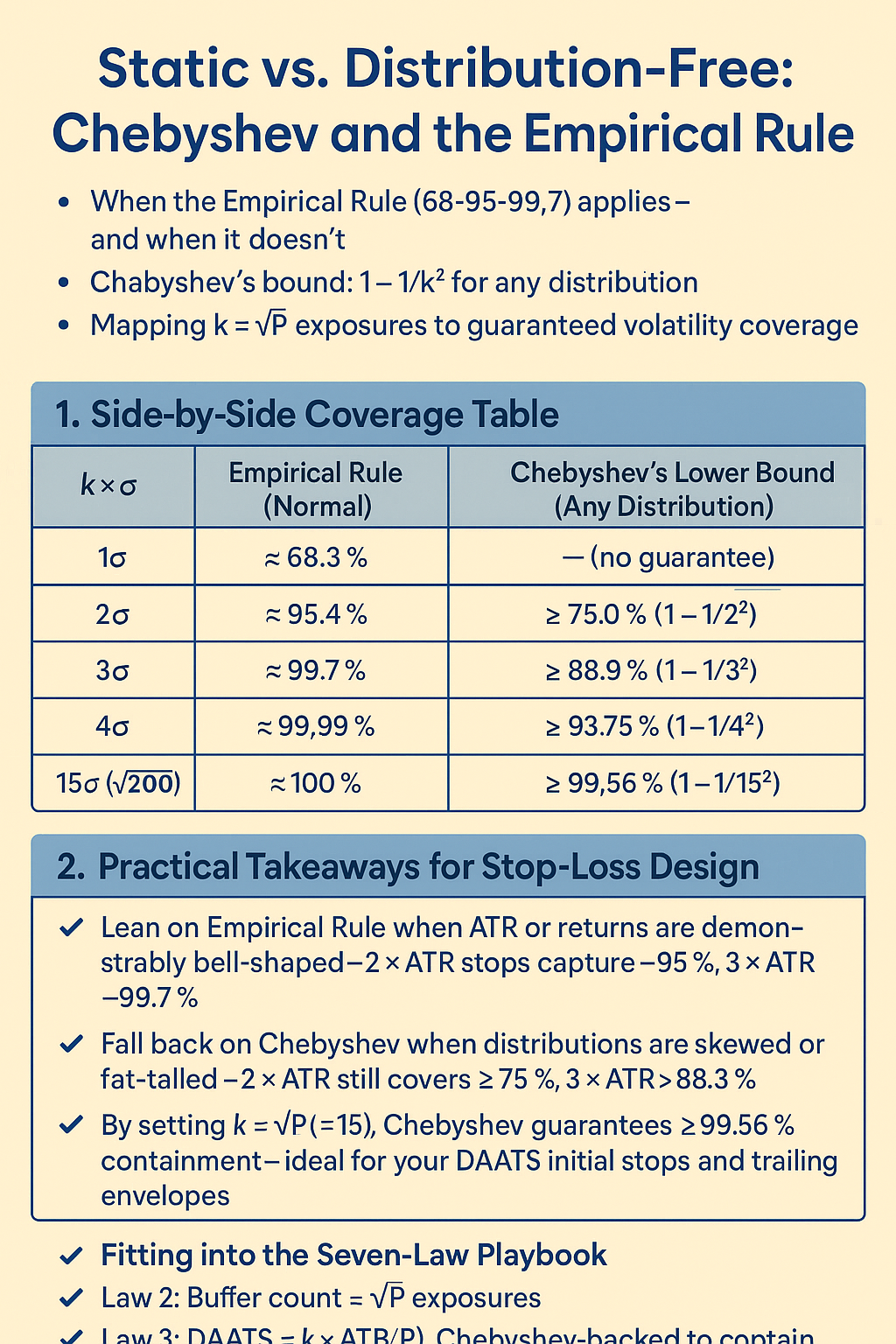
1. Side-by-Side Coverage Table
| k × σ | Empirical Rule (Normal) | Chebyshev’s Lower Bound (Any Distribution) |
|---|---|---|
| 1σ | ≈ 68.3 % | — (no guarantee) |
| 2σ | ≈ 95.4 % | ≥ 75.0 % (1 – 1/2²) |
| 3σ | ≈ 99.7 % | ≥ 88.9 % (1 – 1/3²) |
| 4σ | ≈ 99.99 % | ≥ 93.75 % (1 – 1/4²) |
| 15σ (√200) | ≈100 % | ≥ 99.56 % (1 – 1/15²) |
2. Practical Takeaways for Stop-Loss Design
- Lean on Empirical Rule when ATR or returns are demonstrably bell-shaped—2×ATR stops capture ~95 %, 3×ATR ~99.7 %.
- Fall back on Chebyshev when distributions are skewed or fat-tailed—2×ATR still covers ≥75 %, 3×ATR ≥88.9 %.
- By setting k=√P (≈15), Chebyshev guarantees ≥99.56 % containment—ideal for your DAATS initial stops and trailing envelopes.
3. Fitting into the Seven-Law Playbook
Our Seven Laws use k=√P exposures throughout:
- Law 2: Buffer count = √P exposures
- Law 3: DAATS = k×ATR(P), Chebyshev-backed to contain 99.56 % of noise
- Laws 4–5: Breakeven & trailing distances also use k fractions of ATR
Integrating both coverage theories ensures you can tighten buffers during calm, normal regimes and lean on distribution-free guarantees when markets turn extreme.
About the Author
Dr. Glen Brown, Ph.D. in Investments & Finance, leads Global Accountancy Institute and Global Financial Engineering. With 25+ years in proprietary trading and quantitative research, he developed the GATS framework and this seven-law stop-loss architecture.
Business Model Clarification
Global Accountancy Institute and Global Financial Engineering operate solely as internal proprietary trading firms. We do not offer public courses or advisory services; all methodologies are for in-house research and desk development.
Risk Disclaimer
Trading derivatives and CFDs carries substantial risk. This article is educational only and does not constitute financial advice. Always perform your own due diligence and consult a licensed professional. Past performance does not guarantee future results; trade at your own risk.
Hashtags: #EmpiricalRule #Chebyshev #StopLoss #Volatility #RiskManagement #GATS #DrGlenBrown
Sponsored Content
